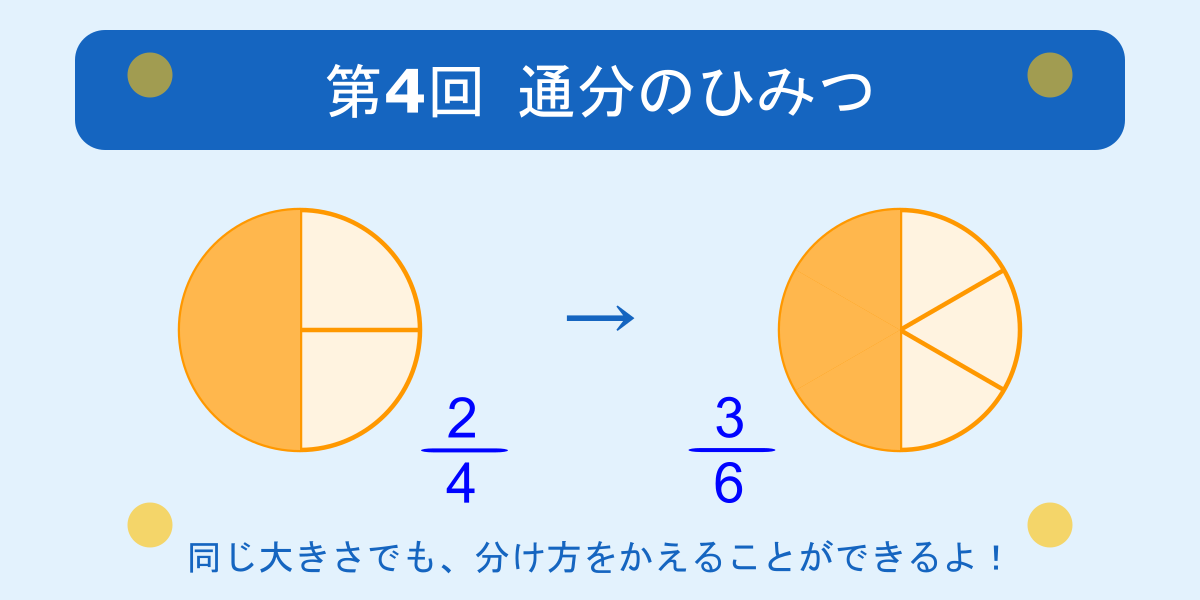
🎯 第4回 通分のひみつ
1️⃣ 違う分母の分数って比べられるの?
2つの分数 \(\frac{1}{2}\) と \(\frac{2}{3}\) 、どちらが大きいかな?
2️⃣ 通分の準備:公倍数を見つけよう!
2と3の最小公倍数は6だね!これを使って通分していくよ。
3️⃣ 通分の魔法を使ってみよう!
⚠️ 大切なポイント
- 分母と分子には同じ数をかけます
- 通分しても分数の大きさは変わりません
- 最小公倍数を使うと計算が楽になります
4️⃣ 比べてみよう!
通分すると \(\frac{3}{6}\) と \(\frac{4}{6}\) になって、比べやすくなったね!
🌈 練習問題
1. 次の分数を通分してみよう:
- \(\frac{2}{3}\) と \(\frac{3}{4}\)
- \(\frac{1}{2}\) と \(\frac{3}{6}\)
2. どちらが大きいかな?
- \(\frac{2}{5}\) と \(\frac{3}{7}\)
- \(\frac{4}{6}\) と \(\frac{5}{9}\)
3. チャレンジ問題:
3つの分数を小さい順に並べてみよう!
\(\frac{2}{3}\), \(\frac{3}{4}\), \(\frac{5}{6}\)
📝 答え
1. 通分の答え:
- \(\frac{2}{3} = \frac{8}{12}\), \(\frac{3}{4} = \frac{9}{12}\)
- \(\frac{1}{2} = \frac{3}{6}\) (もともと同じ大きさ)
2. 大小比較の答え:
- \(\frac{2}{5} = \frac{14}{35}\), \(\frac{3}{7} = \frac{15}{35}\) → \(\frac{2}{5} < \frac{3}{7}\)
- \(\frac{4}{6} = \frac{12}{18}\), \(\frac{5}{9} = \frac{10}{18}\) → \(\frac{5}{9} < \frac{4}{6}\)
3. チャレンジ問題の答え:
\(\frac{2}{3} < \frac{3}{4} < \frac{5}{6}\)
次回は「帯分数の計算」について学びます。お楽しみに!
✨ 練習問題の解説
問題1の解説: \(\frac{2}{3}\) と \(\frac{3}{4}\) の通分
🎯 ステップ1: 分母の最小公倍数を見つけよう
🎯 ステップ2: それぞれの分数を変換しよう
🌟 ポイント
- 分母に掛けた数は、必ず分子にも掛けよう!
- 通分しても分数の大きさは変わらないよ
問題2の解説: \(\frac{2}{5}\) と \(\frac{3}{7}\) の比較
🎯 ステップ1: 5と7の最小公倍数を見つけよう
🎯 ステップ2: 35を分母にして通分しよう
🌟 ポイント
- 分母を35にそろえると比べやすくなるよ
- 分子を見比べると、14 < 15 だから \(\frac{2}{5} < \frac{3}{7}\)
チャレンジ問題の解説
🎯 3つの分数 \(\frac{2}{3}\), \(\frac{3}{4}\), \(\frac{5}{6}\) を通分しよう
🌟 まとめ
- 分母を12にそろえると、分子は 8, 9, 10 になったよ
- 8 < 9 < 10 だから、\(\frac{2}{3} < \frac{3}{4} < \frac{5}{6}\)
/