円の世界へようこそ!
円の基本と大きさを変えてみよう
スライダーを動かして円の大きさを変えてみましょう。半径、直径、円周、面積がどのように変わるか観察しましょう。
半径: 50 mm
直径: 100 mm
円周: 314.16 mm
面積: 7853.98 mm2
クイズの答え
問題1:半径5cmの円の直径は何cmですか?
答え: 10cm (直径 = 半径 × 2 = 5 × 2 = 10cm)
問題2:直径10cmの円の円周は約何cmですか?
答え: 約31.4cm (円周 = 直径 × 円周率 = 10 × 3.14 = 31.4cm)
問題3:半径3cmの円の面積は約何cm2ですか?
答え: 約28.26cm2 (面積 = 半径 × 半径 × 円周率 = 3 × 3 × 3.14 = 28.26cm2)
円の世界へようこそ!
みなさんの周りには、たくさんの「円」があります。お皿、車のタイヤ、時計の文字盤…。 今日は、この「円」についていっしょに学んでいきましょう!
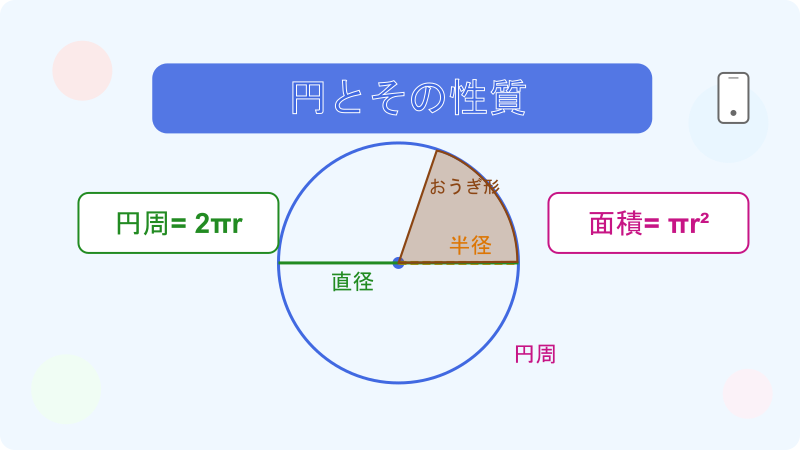
円のひみつ その1:中心と半径
円には「中心」があります。そして、中心から円のどの点までの距離も同じです。 この距離を「半径」と呼びます。
やってみよう!
コンパスを使って円をかいてみましょう。コンパスの針を中心に置き、鉛筆でぐるっと回すと、きれいな円ができあがります。 コンパスの開き具合が「半径」になるんですよ!
円のひみつ その2:直径
円の中心を通って、円上の2点を結ぶ線を「直径」と呼びます。 直径は半径の2倍の長さです。
直径 = 半径 × 2
例えば、半径が5cmの円の直径は、5 × 2 = 10cm になります。
円のひみつ その3:円周
円のまわりの長さを「円周」と呼びます。 円周は直径のおよそ3.14倍になります。この3.14という数を「円周率」と呼びます。
円周 = 直径 × 円周率(3.14)
円周 = 半径 × 2 × 3.14
たしかめてみよう!
コップや缶などの円い物の周りを、ひもで一周測ってみましょう。 次に、直径を定規で測ります。円周÷直径を計算すると、だいたい3.14になるはずです!
円のひみつ その4:円の面積
円の中の面積は、半径を2回かけて、さらに円周率をかけると求められます。
円の面積 = 半径 × 半径 × 円周率(3.14)
円の面積 = 半径2 × 3.14
円を細かく切り分けると、こんな形になります。これを並べ替えると、ほぼ長方形になるんです!
円のひみつ その5:おうぎ形
円を中心から切り分けたピザのような形を「おうぎ形」と呼びます。
おうぎ形の中心角が360度の何分の一かで、おうぎ形の面積や弧の長さを求めることができます。
おうぎ形の面積 = 円の面積 × (中心角 ÷ 360度)
おうぎ形の弧の長さ = 円周 × (中心角 ÷ 360度)
例えば、半径10cmの円で、中心角が90度(360度の1/4)のおうぎ形の面積は:
(10 × 10 × 3.14) × (90 ÷ 360) = 314 × 1/4 = 78.5cm2
円は身の回りにあふれています
円の知識は、私たちの生活のいろいろなところで役立っています。
自転車のタイヤが1回転すると進む距離は、タイヤの円周と同じです。
まとめ:円のひみつを復習しよう
- 半径:円の中心から円周上の点までの距離
- 直径:円の中心を通る線分で、円周上の2点を結ぶもの(半径の2倍)
- 円周:円の周りの長さ(直径 × 円周率)
- 円周率:約3.14という特別な数
- 円の面積:半径 × 半径 × 円周率
- おうぎ形:円を中心から切り分けた形
チャレンジしてみよう!
身の回りから円い形のものを見つけて、その半径、直径、円周、面積を計算してみよう!
クイズに挑戦!
問題1:半径5cmの円の直径は何cmですか?
ヒント:直径は半径の何倍だったかな?
問題2:直径10cmの円の円周は約何cmですか?
ヒント:円周率は約3.14です。
問題3:半径3cmの円の面積は約何cm2ですか?
ヒント:円の面積は半径×半径×円周率です。