第7回:分数のかけ算②と逆数
〜分数の計算がもっと楽しくなる!〜
1逆数ってなんだろう?
みなさん、こんにちは!今日は「逆数」という新しい友だちを紹介します。
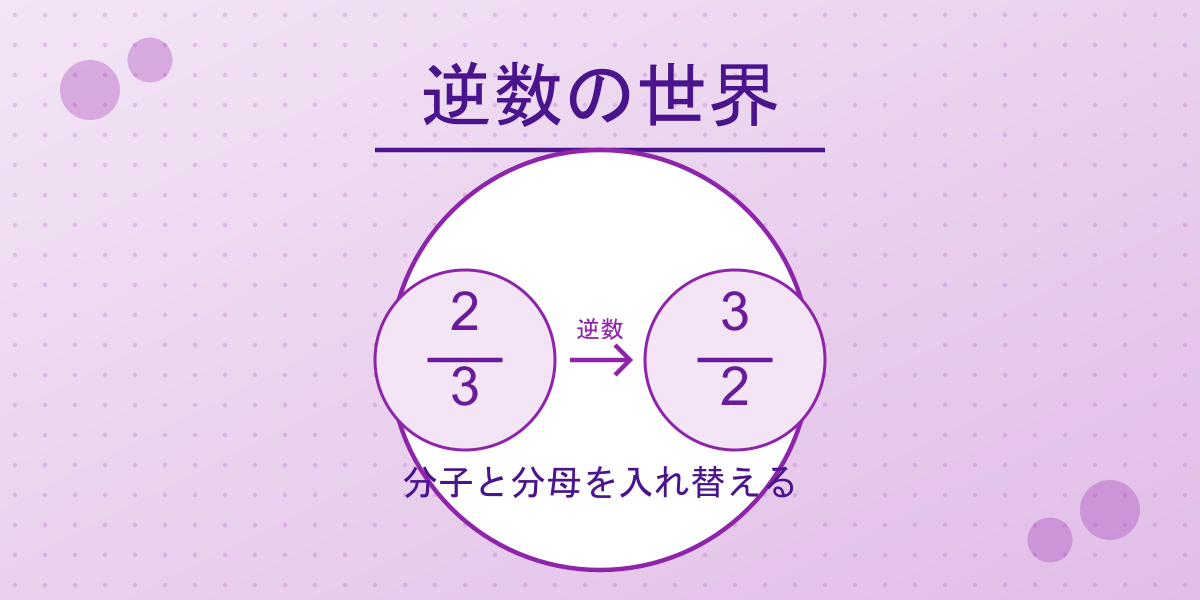
逆数は、分母と分子を入れ替えた数のことです。とっても簡単ですよ!
例えば、$\frac{2}{3}$ の逆数は $\frac{3}{2}$ です。
$\frac{4}{5}$ の逆数は $\frac{5}{4}$ です。
2逆数のかけ算の特徴
逆数どうしをかけ算すると、とっても素敵なことが起こります!
数と その逆数 をかけると、答えは必ず1になります。
例:$\frac{2}{3} \times \frac{3}{2} = 1$
3練習問題
問題1:次の分数の逆数を書きましょう
(1) $\frac{3}{4}$ の逆数は?
(2) $\frac{5}{2}$ の逆数は?
問題2:次の計算をしましょう
(1) $\frac{2}{5} \times \frac{5}{2}$ = ?
(2) $\frac{3}{7} \times \frac{7}{3}$ = ?
4暗算のコツ
暗算のコツ:
1. 分母と分子を頭の中で入れ替えてみよう
2. かけ算をするときは、分子どうし・分母どうしをかけよう
練習問題の答えと解説
問題1の答え:
(1) $\frac{4}{3}$
(2) $\frac{2}{5}$
解説:分母と分子を入れ替えるだけでOKです!
問題2の答え:
(1) $\frac{2}{5} \times \frac{5}{2} = 1$
(2) $\frac{3}{7} \times \frac{7}{3} = 1$
解説:逆数どうしをかけると、必ず1になることを覚えておきましょう!
逆数の便利な使い方を学ぼう!
例1:お菓子分けの場面
たろうくんは、12個のクッキーを友だち3人に同じ数ずつ分けることにしました。
1人分を求めるには、12 ÷ 3 = 4 という計算をします。
これは、$12 \times \frac{1}{3}$ と同じ意味なんです!
わり算は、分数の逆数をかけることで計算できます!
$12 \div 3 = 12 \times \frac{1}{3} = 4$
例2:レシピの材料を調節するとき
4人分のカレーのレシピを2人分に調節したい場合:
すべての材料を$\frac{1}{2}$倍すれば良いですね。
例:玉ねぎ2個 → $2 \times \frac{1}{2} = 1$個
魔法のように簡単!
4人分 → 2人分 = もとの量 × $\frac{1}{2}$
4人分 → 6人分 = もとの量 × $\frac{3}{2}$
例3:時速と距離から時間を求める
時速6kmで走って、3kmの道のりを行くのにかかる時間は?
時間 = 距離 ÷ 速さ
$3 \div 6 = 3 \times \frac{1}{6} = \frac{1}{2}$ 時間(30分)
わり算を逆数のかけ算に変えると、計算が簡単になることがあります!
逆数が便利なわけ
1. わり算を、かけ算に変えられる
2. 分数のわり算が簡単になる
3. 量の調節が分かりやすくなる
覚えておこう!
$a \div b = a \times \frac{1}{b}$
(わり算は、割る数の逆数をかけることと同じ)
練習してみよう!
問題1:6人分のケーキのレシピを3人分に調節するには、材料を何倍すればいい?
問題2:時速4kmで走って、2kmの道のりを行くのにかかる時間は?
答え1:$\frac{1}{2}$倍($6人 \div 2 = 6 \times \frac{1}{2}$)
答え2:$\frac{1}{2}$時間(30分)($2 \div 4 = 2 \times \frac{1}{4} = \frac{1}{2}$)